회귀분석

회귀분석(regression analysis)

 

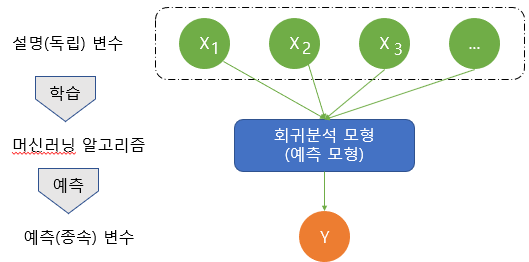
회귀분석은 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법이다.

즉, 종속변수와 독립변수의 관계식을 추론하여 두 변수 간의 인과관계를 파악/예측하는 것이 회귀분석의 목적이다.

가격, 매출, 주가, 환율, 수량 등 연속적인 값을 갖는 연속 변수를 예측하는데 주로 활용될 수 있다.

 

회귀분석 검토사항

용어 정리

1. 귀무가설(=영가설)

- 실험이나 관찰을 통해서 기각하고 싶은 기존의 가설.

- 측정된 값들은 회귀식으로 설명할 수 없다.

- 독립변수는 종속변수에 영향을 주지 않는다.

 

2. 대립가설(=연구가설)

- 실험이나 관찰을 통해서 주장하고 싶은 새로운 이론.

- 측정된 값들은 회귀식으로 설명할 수 있다.

- 독립변수는 종속변수에 영향을 준다.

 

3. 기각

- 통계적으로 유의하다.

- 대립가설이 참이다.

 

4. 기각역

- 확률분포에서 귀무가설을 기각하는 영역.

- 기각역에 검정통계량이 위치하면 귀무가설을 기각함.

- 대부분의 통계에서 p-값 < 0.05 이면 귀무가설을 기각함.

- 회귀모형은 유의하다고 함.

 

5. 유의수준

- 가설을 검정할 때 어느 정도까지 벗어나면 귀무가설이 오류라고 인정하는 수준을 말함.

 

6. 결정계수

- 종속변수의 분산 중에서 독립변수로 설명되는 비율을 의미한다. 쉽게 말해, 이 통계 모델로 대상을 얼마나 잘 설명할 수 있는가를 숫자로 나타낸 것이 결정계수이다.

 

모형이 통계적으로 유의미한가?

→ F 통계량을 확인하여 유의확률(p-값)이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의수준 5%이하에서 유의미하다고 한다.

 

모형의 설명력

→ 결정계수가 0~1 값을 가지며, 높은 값을 가질수록 추정된 회쉬식의 설명력은 높다고 한다.

 

모형의 적합도

→ 잔차 그래프 및 회귀진단으로 판단한다. 잔차 검정은 정규성과 등분산성 가정을 만족하는지에 대한 검토 과정이다.

 

회귀계수들이 유의한가?

→ 회귀계수의 t값과 유의확률(p-값)로 확인한다.